# Ideate
# Dotmocracy
- Purpose
- Evaluate and select ideas democratically
- Time required
- 10 to 30 minutes
- Participants
- Design Thinking team, 1 moderator
- Level of experience
- Beginner
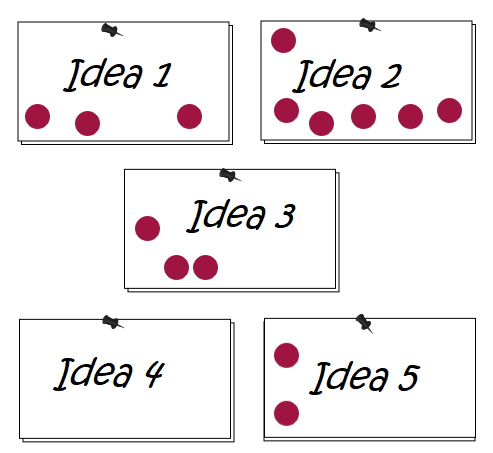
# What is it about?
Dotmocracy, also known as dot voting, is a method to evaluate ideas from the brainstorming phase together in a group.
# The goal
The aim is that each team member has the same voting power when selecting the best ideas and thus the most popular ideas in the team are determined democratically.
# How to do it?
- Record the collected ideas visibly on a board or pinboard.
- The moderator hands out 2 sticky points to all participants.
- Ask the group members to distribute the stickers among their two favorite ideas.
- After all the points have been distributed, the ideas will be sorted by the number of points.
- Discuss the ideas with the most sticky points and develop them further.
- Keep ideas with fewer points as a reserve and discard the ideas without points.
# When do you need it?
The method is suitable after the diverging idea generation phase. It is used when there is a large pool of ideas that need to be narrowed down and selected.
# Resources
- Paper
- Pens
- Sticky points
- Pinboards
- Pins or magnets
# Advantages
This method serves to make decisions quickly, visually, flexibly and easily with the aim to avoid protracted analysis paralysis. Decisions are based on reflection and agreement and NOT based on power, rank, and extroversion. Another advantage is the inclusion of the opinion of everyone involved in the decision-making process.
# Disadvantages
There is a risk of anchor and knock-on effects. It is also beneficial to support the decision with other methods.
# Keep in mind
The entire team benefits from the fact that ideas are evaluated as neutrally as possible, i.e. their own ideas are not preferred. Ask the participants to be open to progressive ideas and not solely vote for what they already know.
# See also
| Previous methods | Alternative methods | Following methods |